Статья расскажет о происхождении термина «Алгоритм» и о том, какими свойствами он обладает.
Алгоритмом называют определенную конечную последовательность действий (набор инструкций), выполнение которых приводит к достижению конкретной цели (решению поставленной задачи). В литературе по информатике, как и на просторах глобальной сети, можно найти множество общей теоретической информации относительно понятия и решения алгоритма. Достаточно запомнить основную мысль: достижение алгоритмического результата обеспечивается выполнением определенной последовательности действий (чаще всего, действий арифметических или логических).
История возникновения термина
Сегодня это понятие является фундаментальным и в математике, и в информатике. Однако сам термин возник задолго до появления компьютеров и прочих электронных средств вычислительной техники. Впервые об алгоритме заговорили в средние века — именно тогда европейские ученые ознакомились с методами вычисления арифметических действий, производимых в десятичной системе счисления азиатским математиком по имени Мухаммед ибн Муса аль-Хорезми (от имени этого математика и сформировался термин Algorithm). Сочинение аль-Хорезми перевели, а в последующие столетия появилось много трудов, посвященных вопросу обучения искусству счёта посредством цифр. Можно вспомнить описание алгоритма в европейской науке в те годы:

Также значение слова «алгоритм» сегодня нередко связывают со значениями таких слов, как «рецепт», «метод», «процесс», «инструкция».
Исполнитель и программа
Судя по историческим справкам, изначально речь шла о способе выполнения арифметических действий над десятичными числами. Прошли годы. Понятие стали применять при обозначении любой последовательности действий, которая приводит к получению требуемого результата. Причем алгоритмы существуют не сами по себе — они предназначаются для конкретного исполнителя. Кто может выступать таким исполнителем:
— человек;
— роботизированное/автоматизированное устройство, механизм;
— компьютер;
— язык программирования и т. д.
Отличительная черта исполнителя — способность выполнять команды, которые включены в алгоритм. Это становится возможным, благодаря описанию последнего на формальном языке, который исключает неоднозначность толкования. Множество команд задано изначально строго и является конечным. Действия, которые должен выполнить исполнитель, называют элементарными действиями, а сама запись алгоритмической последовательности на формальном языке — это программа. Разработка алгоритма в целях решения задачи — это алгоритмизация.
Главные характеристики
Выделяют следующие свойства алгоритма: массовость, дискретность, результативность, определенность, понятность, формальность, завершаемость. Будет не лишним рассмотреть их более подробно, дав каждому свойству алгоритма пояснение:
1. Массовость (универсальность). Благодаря этому свойству, алгоритм можно успешно применять к различным наборам исходных данных. Пусть существует запись некой абстрактной последовательности, выраженная формулой. Подставляя в эту формулу значения (каждый раз новые), пользователь будет получать верные решения в соответствии с определенным алгоритмом действий.
2. Дискретность (разрывность). Это свойство характеризует структуру. Каждая алгоритмическая последовательность действий делится на этапы (шаги), а процесс решения задачи — это последовательное исполнение простых шагов. Также дискретность обозначает, что для выполнения каждого этапа потребуется конечный временной отрезок (исходные данные преобразуются во времени в результат дискретно).
3. Определенность (точность, детерминированность) — это свойство указывает алгоритму, что каждый его шаг должен быть строго определенным, то есть различные толкования должны быть исключены. Строго определяется и порядок выполнения шагов. В результате каждый шаг определяется состоянием системы однозначно, когда четко понятно, какая команда станет выполняться на следующем шаге. Как итог — при любом исполнителе для одних и тех же исходных данных при выполнении одной и той же цепочки команд будет выдаваться одинаковый результат. Да, существуют вероятностные алгоритмы — в них на последующий шаг влияют как текущее состояние системы, так и генерируемое случайное число. Но при включении способа генерации рандомных чисел в перечень «исходных данных», вероятностный алгоритм превращается в подвид обычного.
4. Понятность. Должны быть включены лишь те команды, которые доступны и понятны исполнителю, то есть входят в систему его команд.
5. Формальность. Любой исполнитель действует формально и лишь выполняет инструкции, не вникая в смысл. Он не отвлекается от поставленной задачи и не рассуждает, зачем и почему они нужны. Рассуждениями занимается разработчик алгоритма, задача же исполнителя — просто исполнить предложенные команды и получить результат. «Приказы не обсуждают, а выполняют».
6. Завершаемость (конечность). Если исходные данные заданы корректно, алгоритм завершит свое действие и выдаст результат за конечное число шагов.
7. Результативность. Согласно этому свойству, любой алгоритм должен завершаться конкретными результатами.
Основные виды алгоритмов
В информатике и программировании выделяют много видов алгоритмов. Основные из них:
— линейные (команды выполняются последовательно, одна за одной);
— разветвляющиеся (есть условие, при проверке которого возможно разветвление на несколько параллельных ветвей);
— циклические (предусматривается многократное повторение одних и тех же действий).
Источники:
• https://math-it.petrsu.ru/users/semenova/Informatika/DOC/Sam_Izuch/Algoritm.pdf;
• https://www.sites.google.com/site/algoritmyvidyisvojstva/materialy/materialy-1.
Алгоритм


4.1
Средняя оценка: 4.1
Всего получено оценок: 452.
4.1
Средняя оценка: 4.1
Всего получено оценок: 452.
Теория алгоритмов является одной из базовых концепций, лежащей в основе компьютерной науки. Основы алгоритмизации и программирования изучаются в курсе информатики в 10 классе. Кратко об алгоритмах и их свойствах можно прочитать в данной статье.
Алгоритм
Решение любой сложной задачи проводится в несколько этапов. Все этапы, выполненные последовательно друг за другом и приводящие в итоге к достижению поставленной цели составляют алгоритм. Например, чтобы снять деньги в банкомате, нужно выполнить последовательность действий: вставить карту, ввести пин-код, выбрать в меню программного обеспечения команду «Снятие наличных», ввести требуемую сумму, распечатать чек, вернуться в главное меню или закончить обслуживание карты.
Алгоритм – это базовое понятие в информатике. Он представляет собой набор инструкций, выполнение которых приведет к решению поставленной задачи за конечное число шагов.
термин «Алгоритм» получил свое название от имени знаменитого восточного ученого математика Мухаммеда аль-Хорезми, жившего в восьмом веке в Багдаде. Трактаты аль-Хорезми внесли большой вклад в развитие средневековой науки.

Свойства алгоритма
Алгоритм, как базовое понятие информатики, обладает рядом свойств:
- Массовость предполагает пригодность алгоритма для различных исходных данных.
- Дискретность означает, что каждый этап алгоритма представляет собой законченное действие.
- Однозначность означает, что очередность выполнения этапов алгоритма должна быть одинакова при всех возможных наборах данных.
- Конечность означает, что алгоритм состоит из строго определенного числа шагов.
Способы записи алгоритмов
Алгоритмы можно представлять по-разному. Существую следующие способы записи алгоритмов:
- формульно-словесный – алгоритм задается с помощью естественного разговорного языка с использованием специальных знаков и формул;
- графический – алгоритм воспроизводится с применением графических объектов, выстроенных в виде блок-схемы;
- алгоритмический язык – алгоритм реализован посредством ключевых слов специального алгоритмического языка.

Самым наглядным алгоритмом, является алгоритм, заданный в виде блок-схемы, где каждый шаг представлен определенной геометрической фигурой: прямоугольник заменяет вычислительный процесс, ромбом изображается условие, шестигранник используется для обозначения цикла с известным числом повторов.
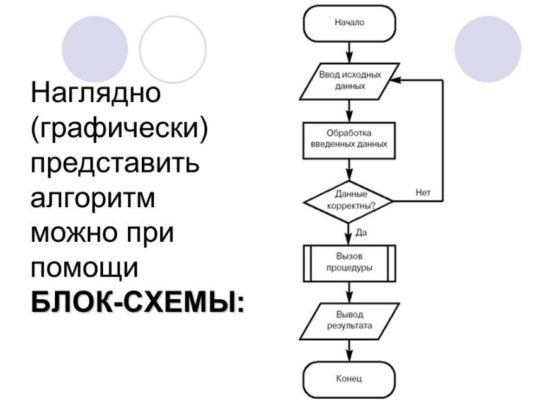
при разработке блок-схем алгоритмов следует пользоваться правилами, регламентированными в специальном стандарте. На территории РФ функционирует Государственный стандарт — ГОСТ 19.701-90 «Схемы алгоритмов программ, данных и систем».
Что мы узнали?
Алгоритм представляет собой цепочку команд, приводящих к определенному результату. Он обладает свойствами массовости, дискретности, конечности, однозначности. Алгоритмы могут быть заданы в виде блок-схем, а также описаны с помощью естественных и специальных алгоритмических языков.
Тест по теме
Доска почёта
Чтобы попасть сюда — пройдите тест.
-
Ольга Титова
4/5
-
Серафима Соломатова
4/5
-
Марик Землянин
5/5
-
Наталья Любимая
5/5
Оценка статьи
4.1
Средняя оценка: 4.1
Всего получено оценок: 452.
А какая ваша оценка?
Материал из «Знание.Вики»
Алгоритм (лат. algorithmi — от имени арабского математика Аль-Хорезми) — это последовательность шагов или инструкций, предназначенных для решения определённой задачи или выполнения определённой операции. Аль-Хорезми считается одним из основателей алгебры и известен благодаря своим работам в области арифметики и алгебры, а также своей книге «Китаб аль-мукаддеса аль-Хорезми», в которой он представил методику решения линейных и квадратных уравнений. Алгоритм является формальным и логически структурированным описанием процесса, который может быть исполнен компьютером, человеком или другим устройством. Применяются во всех областях информатики, математики, логики, экономики и других наук, где требуется решение определённых проблем или выполнение операций[1]. Они являются ключевой составляющей при решении задач и автоматизации процессов. Чтобы быть эффективным, алгоритм должен быть ясным, последовательным и простым для понимания. Он должен определять все необходимые шаги, чтобы достичь результата, и учитывать возможные входные данные и условия.
История термина
Термин «алгоритм» происходит от имени арабского учёного Мухаммеда аль-Хорезми (около 780—850 годов), который жил и работал на территории современного Узбекистана и Ирана. Аль-Хорезми был известным математиком и астрономом, и его основное достижение заключалось в разработке новой системы записи и вычисления чисел, известной как индийская цифровая система.
Учёный также написал книгу «Китаб аль-Мукаддима аль-Хорезми», или «Введение к арифметике». В этой книге он представил новый способ описания решения математических задач, который включал последовательность шагов, которые нужно выполнить для достижения результата. Эти шаги были точными и логическими, и аль-Хорезми использовал термин «алгоритмус» для обозначения этого процесса. В своей работе по алгебре, Аль Хорезми разработал систему записи и решения линейных уравнений и эту систему назвал «аль-джабр ва аль-мукабала», что в переводе с арабского языка означает «восстановление (и решение) и последующая балансировка». Этот термин становится основой для слова «алгебра», которое по-прежнему используется сегодня[1].
Термин «алгоритм» стал широко использоваться в математике и науке в последующие века. В XVII веке появилось понятие алгоритма как последовательности команд, выполняемых для решения математической задачи или получения определённого результата. Считается, что основоположником современной теории алгоритмов является математик Готфрид Лейбниц, который в 1684 году предложил идею символьного исчисления и разработал методы для выполнения вычислений с помощью языка символов. С тех пор понятие алгоритма распространилось на различные области науки и техники, и сейчас используется в широком смысле, охватывая различные методы и процедуры решения задач.
Вплоть до 1930-х годов большинство алгоритмов было разработано в рамках конкретных областей, таких как математика, физика или инженерия. Однако с развитием вычислительной техники и информатики возникла необходимость в строгом математическом определении понятия алгоритма. В 1936 году Алан Тьюринг опубликовал свою работу «Вычислимые числа: машины и интуиция», где он предложил формальное определение алгоритма. В своей работе он вводит понятие «универсальной вычислительной машины», которая может исполнять любой алгоритм. Эта работа стала основой для развития теории алгоритмов и компьютерных наук в целом. Тьюринг показал, что существуют задачи, для которых не существует алгоритма, который бы решал их во всех случаях. Это привело к формированию понятия вычислительной неразрешимости и развитию теории сложности вычислений. Таким образом, с появлением формального определения алгоритма появилась возможность точно определять, является ли тот или иной процесс алгоритмом[2].
В 1950-е годы XX века работы Колмогорова и Маркова принесли значительный вклад в развитие теории алгоритмов. Андрей Колмогоров в своих работах предложил формализацию идеи алгоритма с помощью понятия «колмогоровской сложности» — меры сложности объектов, определяемой длиной наименьшего программного кода, позволяющего их описать. Это понятие имеет важное значение в теории информации и алгоритмической сложности[3]. Андрей Марков разработал свою модель вычислений, которая стала известна как модель «машин Маркова». Эта модель позволила формально описывать алгоритмические процессы и решать различные задачи, связанные с последовательностями и автоматами.
Сегодня алгоритм используют для обозначения набора инструкций, которые могут быть выполнены для решения определённой задачи. Алгоритмы используются в различных областях, включая математику, информатику, программирование, искусственный интеллект и технологии. Они являются основным инструментом для разработки программ, создания компьютерных моделей и решения сложных задач.
Определение
Точное определение понятия алгоритма имеет большое значение для развития физики и техники. Оно позволяет разрабатывать более эффективные алгоритмы вычислений, которые могут быть использованы в различных областях, таких как искусственный интеллект, криптография, оптимизация и многое другое, а также в разработке программного обеспечения. Они используются для решения различных задач, начиная от сортировки данных и поиска информации, до оптимизации производительности и разработки искусственного интеллекта. Хороший алгоритм должен быть чётким, последовательным и решать задачу эффективно.
1. В информатике: алгоритм — это чётко определённая последовательность инструкций, выполняющихся с целью решения определённой задачи. Алгоритм должен быть корректным, то есть приводить к правильному решению, а также быть эффективным, чтобы решение было достигнуто за разумное время.
2. В математике: алгоритм — это формально определённый вычислительный процесс, состоящий из конечного набора шагов. Алгоритм должен быть выполняемым и всегда завершаться, а также давать одинаковые результаты при одинаковых входных данных[4].
3. В общем смысле: алгоритм — это последовательность шагов или инструкций, описывающих порядок выполнения определённых действий. Это может быть любая систематизированная процедура, используемая для достижения конкретной цели или решения задачи. Он представляет собой конкретный план действий, который нужно выполнить для получения желаемого результата[2].
Свойства алгоритма
Свойства алгоритма могут включать следующие аспекты:
1. Корректность: алгоритм должен давать верный результат для всех возможных входных данных. Он должен выполнять все требования поставленной задачи и не допускать ошибок.
2. Однозначность: каждый шаг алгоритма должен быть определён и ясно понятен.
3. Дискретность: алгоритм — состоит из отдельных маленьких шагов, или действий. Эти действия идут в определённом порядке, одно начинается после завершения другого[5].
4. Производительность: алгоритм должен использовать доступные ресурсы (например, память и процессорное время) эффективно и экономно. Он определяет время выполнения и объём затраченных ресурсов (например, памяти или вычислительной мощности). Её можно измерить с помощью сложности алгоритма.
5. Понятность: алгоритм должен быть понятен и включать команды, понятные для исполнителя, которые будут его анализировать или использовать.
6. Детерминированность: инструкции должны быть чётко определены и не должно возникать разночтений и разногласий ни на одном из этапов выполнения алгоритма[5].
7. Результативность: завершение алгоритма приводит к определённым результатам.
8. Эффективность: алгоритм должен быть выполнен с использованием минимально возможных ресурсов и требовать наименьшего количества операций или вычислений для решения задачи. Он должен работать быстро и занимать небольшой объём памяти.
Важной особенностью алгоритма является его универсальность. То есть алгоритм должен быть применим к любой задаче данного типа, не зависимо от её сложности или разнообразия. Эти свойства являются важными при выборе и оценке алгоритмов, так как они напрямую влияют на его работоспособность и эффективность в решении поставленных задач.
Виды алгоритмов
Существует множество различных видов алгоритмов, включая:
- Линейный алгоритм — это алгоритм, который выполняет каждое действие по очереди и без пропусков. Линейный алгоритм последовательно выполняет инструкции без перехода к другим частям программы, пока не достигнет конца. Такие алгоритмы разработаны для простых и последовательных задач, где каждое действие зависит от предыдущего и не требуется сложной логики или принятия решений.
- Циклический алгоритм — это алгоритм, который выполняется в цикле до выполнения какого-то условия, являются основой для многих программ и позволяют повторять операции множество раз без необходимости повторного написания кода. Циклические алгоритмы используются для обработки повторяющихся задач или для выполнения итераций по коллекциям данных. Циклические алгоритмы могут также использоваться для обхода коллекций данных, таких как массивы или списки. В этом случае цикл выполняется для каждого элемента коллекции.
- Разветвляющийся алгоритм — это алгоритм, в котором происходит ветвление на несколько направлений выполнения в зависимости от условий. Он позволяет программе принимать решения на основе различных ситуаций и выполнять соответствующие действия[6].
- Блок-схема — это графическое представление последовательности операций или шагов в алгоритме или процессе. Она состоит из блоков, которые представляют операции, принятия решений или ввод-вывод данных, и связей между блоками, обозначающих последовательность выполнения[7].
- Графы и деревья — алгоритмы для работы с графами и деревьями, включающие поиск пути между вершинами, обходы графов и деревьев, поиск минимального остовного дерева и т. д.
- Вспомогательный алгоритм — это алгоритм, который используется внутри другого алгоритма для выполнения определённой подзадачи или облегчения выполнения основной задачи. Он может выполнять различные операции и иметь разные цели, в зависимости от контекста, в котором используется. Например, вспомогательный алгоритм может выполнять сортировку данных перед их обработкой другим алгоритмом, вычислять промежуточные значения или проверять определённые условия. Вспомогательные алгоритмы часто используются для разделения сложных задач на более простые подзадачи, что упрощает понимание и реализацию основного алгоритма. Они также позволяют повторно использовать код и ускорить выполнение основного алгоритма, освобождая его от необходимости выполнять одни и те же операции несколько раз[8].
- Рекурсивный алгоритм — это алгоритм, вызывающий себя до тех пор, пока не будет достигнуто некоторое условие возращения.
Способы представления алгоритмов
Выбор способа представления алгоритма зависит от его сложности, целевой аудитории и контекста использования. Комбинирование разных способов представления может быть полезным для более полного и понятного описания алгоритма.
1. Словесная форма: алгоритм описывается в виде последовательности шагов на естественном языке, где каждый шаг описывает конкретное действие или операцию. Это наиболее распространённый и понятный способ представления алгоритма.
2. Язык программирования — формальный язык, который используется программистами для написания программ компьютерных приложений. Язык программирования определяет набор правил и синтаксис для создания кода, который затем может быть скомпилирован или интерпретирован на компьютере. Примеры популярных языков программирования включают C, C++, Java, Python, JavaScript, Ruby и многие другие. Каждый язык имеет свои особенности и применяется для решения определённых задач в различных областях разработки программного обеспечения[9].
3. Псевдокод — это упрощённый язык программирования, который использует общепринятые конструкции и синтаксис для описания алгоритмов. Он позволяет более точно и формально описывать алгоритмы, но без привязки к конкретному языку программирования.
4. Блок-схема: алгоритм представляется в виде графического обозначения, где каждый блок представляет отдельный шаг, а стрелки указывают на последовательность выполнения шагов. Это визуальный способ представления алгоритма, который позволяет наглядно представить его структуру. Блок-схемы часто используются для более наглядного представления сложных алгоритмов или для обучения программированию[8].
Примечания
- ↑ 1,0 1,1 Алгоритм. Большая российская энциклопедия. Большая российская энциклопедия (10 августа 2022). Дата обращения: 30 октября 2023.
- ↑ 2,0 2,1 Игошин В. И. Теория алгоритмов. — М.: ИНФРА-М, 2016. — С. 6—22. — 318 с. — ISBN 978-5-16-005205-2.
- ↑ Вьюгин В.В. Колмогоровская сложность и алгоритмическая теория информации. Институт проблем передачи информации РАН. Дата обращения: 1 ноября 2023.
- ↑ Алгоритм. БСЭ. Большая Советская Энциклопедия 3 изд. том 1. Дата обращения: 30 октября 2023.
- ↑ 5,0 5,1 Алгоритм — что это такое: виды и типы алгоритмов, применение. Skillfactory media (19 августа 2023). Дата обращения: 31 октября 2023.
- ↑ Жданова Т. А. Основы алгоритмизации и программирования. Тихоокеанский государственный университет. Издательство ТОГУ. Дата обращения: 31 октября 2023.
- ↑ НОУ ИНТУИТ | Лекция | Понятие алгоритма. Виды алгоритмов. Национальный Открытый Университет «ИНТУИТ». Дата обращения: 31 октября 2023.
- ↑ 8,0 8,1 Горностаева Т.Н. Алгоритм. — М.: Мир науки, 2019. — С. 10—13. — 64 с. — ISBN 978-5-6043306-3-0.
- ↑ Языки программирования: характеристика, описание, виды OTUS (11 сентября 2022). Дата обращения: 30 октября 2023.
Цель занятия: познакомить учащихся
с понятием алгоритма, исполнителями алгоритмов,
примерами алгоритмов в жизни, алгоритмическим
способом решения задач, закрепить полученные
знания с помощью электронного теста, развивать
навыки самоконтроля.
Ход урока
- Организационный момент.
- Подготовка к изучению нового материала.
(ознакомление с планом и целью занятия) . - Изучение нового материала. (просмотр
электронного урока с использованием мультимедиа
проектора) . Слайды + текст лекции. - По ходу урока учащиеся конспектируют
определения и отвечают на вопросы. - Закрепление темы занятия (работа уч-ся на
компьютере) . Электронный тест с последующей
самопроверкой. Решение алгоритмических задач. - Подведение итогов. Выставление оценок с учетом
процентного выполнения теста. - Задание на дом. (выучить определения, привести
примеры алгоритмов из жизненной практики.)
Изучение нового материала.
Один из важнейших этапов решения задач на
ЭВМ – составление алгоритма. О том, что такое
алгоритмы, какими общими свойствами они обладают
и как исполняются, мы и поговорим на этом уроке.
В 1983 году отмечалось 1200-летие со дня рождения
одного из величайших ученых Средней Азии и
средневекового Востока Мухамада ибн Мусы
аль-Хорезми. Он написал ряд трактатов по
арифметике и алгебре, в том числе книгу
«Арифметика индусскими цифрами» – о
счете с помощью десяти цифр и правилах
арифметических действий с числами.
Имя ученого аль-Хорезми превратилось в понятие
algorithmi, первоначально обозначавшее десятичную
систему исчисления и правила арифметических
действий в этой системе. Отсюда и возник
современный научный термин «алгоритм».
Каждый из нас ежедневно использует различные
алгоритмы: инструкции, правила, рецепты и т.п.
Обычно мы это делаем не задумываясь. Например,
открывая дверь ключом, никто не размышляет над
тем, в какой последовательности выполнять
действия. Однако чтобы научить кого-нибудь
открывать дверь, придется четко указать и сами
действия, и порядок их выполнения. То же
потребуется и при указании маршрута поездки.
Сравним эти алгоритмы. На первый взгляд, между
ними нет ничего общего. Одно дело – открывать
дверь, другое – ехать в гости. Но если
приглядеться внимательно, можно заметить
существенное сходство между ними. Прежде всего,
это строгий порядок выполнения действий.
Демонстрация слайда 1.
/Приложение/
Мы можем теперь сказать, что алгоритм – это
организованная последовательность действий.
Данную формулировку, конечно, нельзя считать
определением алгоритма. Например, мы не
объяснили, что означают слова
«организованная» и «действия». Скажем
сразу: абсолютно строгого определения алгоритма
не существует. Алгоритм – это одно из тех
основных понятий (категорий) математики, которые
не обладают формальным определением в терминах
более простых понятий, а абстрагируются
непосредственно из опыта.
На слайде еще одно задание. Выполните его,
используя для записи ответа любой текстовый
редактор или бумагу и карандаш.
Демонстрация слайда 2. /Приложение/
Сравните свой ответ с правильным.
Правильный алгоритм:
- Налить в чайник воду.
- Зажечь спичку.
- Открыть кран газовой горелки.
- Поднести спичку к горелке.
- Поставить чайник на плиту.
- Ждать, пока вода закипит.
- Выключить газ.
Демонстрация слайда 3. /Приложение/
Рассмотренные нами алгоритмы составлены для
исполнения человеком. Но человек далеко не
единственный возможный исполнитель алгоритмов.
Все живые существа и даже отдельные клетки
исполняют различные алгоритмы. Способны на это и
созданные человеком устройства –
роботы-манипуляторы и станки с программным
управлением. Но прежде чем составлять алгоритм
решения задачи, нужно узнать, какие действия
предполагаемый исполнитель способен выполнить.
Поясним сказанное на примере. Допустим, нужно
решить квадратное уравнение.
Десятикласснику требуется минимум инструкций,
потому что он уже знает способ решения.
Восьмикласснику понадобятся намного более
сложные инструкции, потому что он этого еще не
проходил.
Теперь мы можем уточнить понятие алгоритма: это
организованная последовательность действий,
допустимых для некоторого исполнителя.
Рассмотрим информационный процесс
редактирования текста. При работе с текстом
возможны различные операции: удаление,
копирование, перемещение или замена его
фрагментов. Что необходимо для того, чтобы
преобразовать текст?
- Первое. Требуется исполнитель.
- Второе. Процесс должен быть разбит на этапы,
понятные исполнителю. - Третье. Должно быть определено начальное
состояние текста и его требуемое конечное
состояние.
Теория алгоритмов имеет большое практическое
значение. Алгоритмический тип деятельности
важен не только как одна из эффективных форм
труда человека. Через алгоритмизацию, через
расчленение сложных действий на всё более
простые, на действия, выполнение которых
доступно машинам, пролегает путь к автоматизации
различных процессов.
Далее под алгоритмом будет пониматься конечная
последовательность указаний, адресованных
исполнителю, четко и однозначно задающая процесс
решения задач какого-либо типа во всех деталях и
позволяющая получить за конечное число шагов
результат, однозначно определяемый исходными
данными.
Такое свойство алгоритма, как однозначность
результата при заданных исходных данных,
называется определенностью
(детерминированностью) .
Заметим, что большинство алгоритмов могут
выполняться при достаточно разнообразных
наборах исходных данных, то есть использоваться
для решения не какой-либо одной задачи, а целого
класса подобных задач. Это свойство алгоритма
называется массовостью.
С алгоритмами человек встречается на каждом
шагу.
Пример 1. Дан угол. Необходимо провести
биссектрису. (Есть способ, как, пользуясь
линейкой и циркулем, можно решить эту задачу.)
Пример 2. Даны два целых числа. Необходимо
найти их разность. (Имеется правило, в котором
ясно изложен весь порядок действий с цифрами
данных чисел.)
В приведенных примерах речь идет о том, как
сложную работу представить в виде
последовательности простых действий. Вычитание
многоразрядных чисел сводится к действиям с
цифрами. При делении угла пополам выполняются
несложные построения линейкой и циркулем.
Однако высказанные соображения следует
дополнить. Ведь правила вычитания формулируются
для любых многоразрядных чисел, а не для каких-то
конкретных двух. Инструкция проведения
биссектрисы тоже такова, что, пользуясь ею, можно
разделить пополам любой угол. То есть каждому
алгоритму присуща массовость –
пригодность для решения не какой-либо одной, а
целого класса задач.
Далее под алгоритмом будет пониматься конечная
последовательность указаний, адресованных
исполнителю, четко и однозначно задающая процесс
решения задач какого-либо типа во всех деталях и
позволяющая получить за конечное число шагов
результат, однозначно определяемый исходными
данными.
Такое свойство алгоритма, как однозначность
результата при заданных исходных данных,
называется определенностью
(детерминированностью) .На этом занятии мы
познакомились с такими важнейшими понятиями, как
алгоритм, исполнитель, система команд
исполнителя, узнали основные свойства
алгоритма.
Закрепление темы:
Алгоритмические задачи
№1. Старик должен переправить на лодке через
реку волка, козу и капусту. Лодка может выдержать
только старика и одного “пассажира”. В каком
порядке старик перевезет пассажиров? Не забудь,
что волк может съесть козу, а коза – капусту.
Найди 2 варианта решения.
Алгоритм решения задачи:
| 1 вариант | 2 вариант |
| 1) __________________________ | 1) _________________________ |
| 2) _________________________ | 2) _________________________ |
| 3) __________________________ | 3) _________________________ |
и т.д.
№2 Два мальчика и двое взрослых должны
переправиться на другую сторону реки на плоту,
который выдерживает либо двух мальчиков, либо
одного мальчика и одного взрослого. Как
осуществить переправу? Найди несколько способов
решения этой задачи.
Алгоритм решения задачи:
| 1 способ | 2 способ | 3 способ | |
| 1 шаг | |||
| 2 шаг | |||
| 3 шаг | |||
| 4 шаг | |||
| 5 шаг |
Обозначения: 1м- один мальчик, 2м – два мальчика,
1в – один взрослый.
1. Практикум по решению задач
Злоумышленник поменял местами действия в
алгоритме вычисления среднего арифметического
из квадратного корня трёх чисел:
Присвоить а значение (а2+в2+с2)
/3.
Вести а,в,с
Сообщить “Среднее арифметическое квадратов
равно”
Сообщить а.
Восстановите правильный порядок действий.
2. Исправьте следующий алгоритм решения
уравнения (х-2) (х+2) =0:
Присвоить х значение +-2.
Сообщить “Корни уравнения равны”.
Сообщить первое значение х.
Сообщить второе значение х.
3. Автомобиль проехал три участка пути разной
длины с разными скоростями. Составьте алгоритм
нахождения средней скорости автомобиля.
4. Проснувшись утром, школьник почувствовал
недомогание. Находившийся рядом злоумышленник
тут же составил для него следующий алгоритм:
Измерить температуру.
Если температура выше 370, то:
Вызвать врача.
Пойти в школу.
Несмотря на недомогание, школьник исправил
этот алгоритм, добавив всего две строки. Какие
строки добавил школьник?
5. Запишите в виде алгоритмов правила
определения знака:
А) произведения двух действительных чисел;
Б) суммы двух действительных чисел.
6. В записи алгоритма вычисления значения
выражения (х2— 5х+5) / (х6— 4х2+3)
Злоумышленник одно действие поставил не на
свое место. Вот как стал выглядеть алгоритм:
- ввести х
- если х6— 4х2 + 3=0, то:
- сообщить “При таком х значение выражения не
определено”. - иначе:
- присвоить у значение (х2— 5х +5) /(х6—
4х2+3) . - конец ветвления.
- сообщить у.
Верните действие на свое место.
Электронный тест
1.Которые из документов являются алгоритмами?
а) Правило правописания приставок,
оканчивающихся на з,с(да)
б) Программа телепередач
в) Кулинарный рецепт приготовления блюда
г) Инструкция по сборке проданного в
разобранном виде шкафа
2. В каких случаях правильно заканчивается
предложение: Алгоритм – это
а) конечная последовательность действий,
приводящая к искомому результату при любых
допустимых исходных данных
б) указание на выполнение действий
в) конечный набор понятных некоторому
исполнителю команд, выполнение которых приводит
к однозначному решению поставленной задачи
г) программа в машинных кодах
3. Расчлененность алгоритма на отдельные
элементарные действия – это
а) Дискретность
б) Определенность
в) Массовость
г) Детерминированность
4. Которые из документов являются алгоритмами?
А) Каталог книг в библиотеке
Б) Порядок набора международного телефонного
номера
В) Рецепт приготовления клея
Г) Настенный календарь на текущий год
Подведение итогов. Выставление оценок с учетом
процентного выполнения теста.
Задание на дом. (выучить определения, привести
примеры алгоритмов из жизненной практики.)
Алгоритм и его свойства
Понятие алгоритма
Одним из фундаментальных понятий в информатике является понятие алгоритма. Происхождение этого термина связано с математикой. Еще на самых ранних ступенях развития математики (Древний Египет, Вавилон, Греция) в ней стали возникать различные вычислительные процессы чисто механического характера. С их помощью искомые величины ряда задач вычислялись последовательно из исходных величин по определенным правилам и инструкциям. Со временем все такие процессы в математике получили название алгоритмов.
Термин алгоритм происходит от имени средневекового персидского математика Мухаммеда Аль-Хорезми (787 – 850 гг.), который еще в IX в. (825 г.) дал правила выполнения четырех арифметических действий в десятичной системе счисления. Процесс выполнения арифметических действий был назван алгоризмом.
С 1747 г. вместо слова алгоризм стали употреблять алгорисмус, смысл которого состоял в комбинировании четырех операций арифметического исчисления – сложения, вычитания, умножения, деления.
К 1950 г. алгорисмус стал алгорифмом. Смысл алгорифма чаще всего связывался с алгорифмами Евклида – процессами нахождения наибольшего общего делителя двух натуральных чисел, наибольшей общей меры двух отрезков и т.п.
Под алгоритмом понимали конечную последовательность точно сформулированных правил, которые позволяют решать те или иные классы задач. Это определение не является строго математическим, так как в нем не содержится точной характеристики того, что следует понимать под классом задач и под правилами их решения.
Первоначально для записи алгоритмов пользовались средствами обычного языка (словесное представление алгоритмов).
Примеры алгоритмов
- Вычислить факториал числа n (произведение n натуральных чисел c=n!), который вычисляется по формуле c=1*2*3*4*…*n
Алгоритм:
- Полагаем c=1 и переходим к следующему пункту.
- Полагаем i=1 и переходим к следующему пункту.
- Полагаем c=i*c и переходим к следующему пункту.
- Проверяем, равно ли i числу n. Если i=n, то вычисления прекращаем. Если i<n, то увеличиваем i на 1 и переходим к пункту 3.
- Найти наименьшее число M в последовательности из n чисел a1, a2,…, an (n?0) . Прежде чем записать словесный алгоритм данного примера, детально рассмотрим сам процесс поиска наименьшего числа. Первоначально в качестве числа M принимается число a1, т.е. полагаем M=a1, после чего M сравниваем с последующими числами последовательности, начиная с a2. Если M? a2, то M сравнивается a3; если M? a3 , то M сравнивается a4; и так до тех пор, пока найдется число ai < M. Тогда полагаем M= ai и продолжаем сравнение с M последующих чисел из последовательности, начиная с ai+1, до тех пор, пока не будут просмотрены все n чисел. В результате просмотра всех чисел M будет иметь значение, равное наименьшему числу последовательности (i – текущий номер числа).
Алгоритм:
- Полагаем i=1 и переходим к следующему пункту.
- Полагаем M= ai и переходим к следующему пункту.
- Сравниваем i с n; если i< n, то переходим к пункту 4; если i= n, то процесс поиска останавливаем.
- Увеличиваем i на 1 и переходим к следующему пункту.
- Сравниваем ai с M. Если M? ai, то переходим к пункту 3; иначе (M >ai) переходим к пункту 2.
Алгоритмы, в соответствии с которыми решение поставленных задач сводится к арифметическим действиям, называются численными алгоритмами (первый алгоритм).
Алгоритмы, в соответствии с которыми решение поставленных задач сводится к логическим действиям, называются логическими алгоритмами (второй алгоритм, поиск пути в лабиринте и др.).
Алгоритм – это понятное и точное предписание (указание) исполнителю совершить определенную последовательность действий для достижения указанной цели или решения поставленной задачи (приводящую от исходных данных к искомому результату).
Свойства алгоритмов
Разработать алгоритм означает разбить задачу на определенную последовательность шагов. От разработчика алгоритма требуется знание особенностей и правил составления алгоритмов.
Каждое указание алгоритма предписывает исполнителю выполнить одно конкретное действие. Исполнитель не может перейти к выполнению следующей операции, не закончив полностью выполнения предыдущей. Поочередное выполнение команд алгоритма за конечное число шагов приводит к решению задачи, к достижению цели. Разделение выполнения решения задачи на отдельные операции, выполняемые исполнителем по определенным командам – важное свойство алгоритмов, называемое дискретностью.
Алгоритм представляет собой последовательность команд (инструкций, директив), определяющих действия исполнителя (субъекта или управляемого объекта). Исполнитель, выполняя алгоритм, может не вникать в смысл того, что он делает, и вместе с тем получать нужный результат. В этом случае говорят, что исполнитель действует формально, т.е. отвлекается от содержания поставленной задачи и строго выполняет инструкции. Таким образом, возможность решения задачи, механически исполняя команды алгоритма в указанной последовательности, называется формальностью.
Всякий алгоритм составляется в расчете на конкретного исполнителя с учетом его возможностей. Для того чтобы алгоритм мог быть выполнен, нельзя включать в него команды, которые исполнитель не в состоянии выполнить. Нельзя повару поручать работу токаря, какая бы подробная инструкция ему не давалась. У каждого исполнителя имеется свой перечень команд, которые он может исполнить. Каждая команда алгоритма должна определять однозначно действие исполнителя. Такое свойство алгоритмов называется определенностью (или точностью) алгоритма.
Алгоритм, составленный для конкретного исполнителя, должен включать только те команды, которые он может выполнить. Это свойство алгоритма называется понятностью. Алгоритм не должен быть рассчитан на принятие каких-либо самостоятельных решений исполнителем, не предусмотренных алгоритмом.
Еще одно важное требование, предъявляемое к алгоритмам, – результативность (или конечность) алгоритма. Оно означает, что исполнение алгоритма должно закончиться за конечное число шагов.
Разработка алгоритмов – процесс творческий, требующий умственных усилий и затрат времени. Поэтому предпочтительно разрабатывать алгоритмы, обеспечивающие решения всего класса задач данного типа. Например, если составляется алгоритм решения кубического уравнения ax3 + bx2 + cx + d = 0, то он должен быть вариативен, т.е. обеспечивать возможность решения для любых допустимых исходных значений коэффициентов a, b, c, d. Про такой алгоритм говорят, что он отвечает требованию массовости.
Основные особенности и свойства алгоритмов:
- Наличие ввода исходных данных.
- Наличие вывода результата выполнения алгоритма, поскольку цель выполнения алгоритма – получение результата, имеющего вполне определенное отношение к исходным данным.
- Дискретность – разбивка алгоритма на элементарные команды, и выполнение очередной команды начинается после завершения предыдущей.
- Формальность – свойство, позволяющее любому исполнителю, способному воспринимать и выполнять отдельные указания алгоритма, правильно выполнить весь алгоритм.
- Определенность (точность) – однозначность предписанной последовательности действий, не допускающей ее двоякого толкования.
- Понятность – свойство, предусматривающее то, что алгоритм должен состоять только из тех команд, которые исполнитель может выполнить.
- Результативность (конечность) – исполнение алгоритма должно закончиться за конечное число шагов.
- Корректность – алгоритм должен задавать правильное решение задачи.
- Массовость – алгоритм разрабатывается для решения некоторого класса задач, различающихся исходными данными.
- Эффективность – алгоритм должен выполняться за разумное конечное время. При этом выбирается наиболее простой и короткий способ решения задачи при соблюдении всех ограничений и требований к алгоритму.
Свойства дискретности, формальности, точности, понятности и конечности являются необходимыми (иначе это не алгоритм). Свойство массовости не является необходимым свойством алгоритма, оно скорее определяет его качество.
Формы записи алгоритмов
Алгоритмы можно записывать по-разному. Форма записи, состав и количество операций алгоритма зависит от того, кто будет исполнителем этого алгоритма.
Способы описания алгоритма:
- Формульная запись
- Табличная запись
- Развернутая словесная
- На алгоритмическом языке
- Графический (в виде блок схемы)
- На языке программирования
-
- Формульная запись алгоритма производится с помощью простых математических, химических, физических формул.
Например:
S=V*t; V=S/t; t=S/V
-
- Табличная запись производится с помощью букв латинского алфавита и знака, который называется знаком присвоения :=.
Например:
| ШАГ | ОПИСАНИЕ ДЕЙСТВИЙ |
| 1. | a:=5x |
| 2. | b:=a+3 |
| 3. | c:=4x |
| 4. | d:=c-7 |
| 5. | y:=b/d |
-
- Развернутое (словесное) описание алгоритма производится на любом национальном языке, единственным условием является соблюдение свойств алгоритма. Используется обычно для описания алгоритмов, предназначенных исполнителю – человеку. Команды записываются на обычном языке и выполняются по порядку. В командах могут использоваться формулы, специальные обозначения, но каждая команда должна быть понятна исполнителю. Естественный порядок команд может быть нарушен, в этом случае команды можно нумеровать и указывать команду, к которой требуется перейти.
Например:
| ШАГ | ОПИСАНИЕ ДЕЙСТВИЙ |
| 1. | число 7 умножить на переменную x |
| 2. | из результата шага 1 вычесть число 4 |
| 3. | число 5 умножить на переменную x |
| 4. | к результату шага 3 прибавить число 3 |
| 5. | результат шага 2 разделить на результат шага 4 |
-
- Запись алгоритма на алгоритмическом языке записывается с помощью служебных слов, языка и формул (знаков присвоения).
Например: найти большее из трех чисел.
Алгоритм БИТ
- чтение a, b, c
- если a < b к 4
- y:=b; к 5
- y:=a
- если y > c к 7
- y:=c
- запись y
- конец
-
- Запись алгоритма в виде блок-схем (или графическая запись). Алгоритмы представляются в виде блок-схем. Существуют специальные стандарты для построения блок-схем, где определяются графические изображения блоков. Команды алгоритмов записываются внутри блоков на обычном языке или с использованием математических формул. Блоки соединяются по определенным правилам линиями связи, которые показывают порядок выполнения команд.
-
- На языке программирования. Если алгоритм разработан для решения задачи на ЭВМ, то для того, чтобы он мог выполниться исполнителем – ЭВМ, его необходимо записать на языке, понятном этому исполнителю. Для этого разработано множество языков программирования для решения задач разных классов. Запись алгоритма на языке программирования называется программой.
Контрольные вопросы
- Что такое алгоритм?
- Перечислите основные особенности алгоритмов.
- Назовите способы представления алгоритмов.
