В начале урока давайте
вспомним, что такое алгоритм.
Алгоритм –
это строгий порядок правил, которые определяют последовательность шагов
обработки информации.
Ранее говорилось о том,
что люди хотели создать машину, которая будет исполнять формальный алгоритм без
помощи человека.
Для создания такой машины
необходимо было выполнить некоторые условия: соответствие техническим
требованиям; доскональное изучение работы алгоритма для обработки информации;
разработка формализованного способа представления таких алгоритмов.
На этом уроке мы
познакомимся с моделями алгоритмических машин в теории алгоритмов, а также
вспомним свойства алгоритма.
Само понятие алгоритма
исследовалось и совершенствовалось на протяжении многих лет. Но несмотря на все
усилия, строгого определения понятия «алгоритм» не было. Поэтому начали появляться
различные определения алгоритма. Но в тоже время все они были равнозначными.
Например, Андрей
Николаевич Колмагоров, русский советский математик предложил следующее
определение: алгоритм – это всякая система вычислений, выполняемых по
строго определённым правилам, которая после какого-либо числа шагов заведомо
приводит к решению поставленной задачи.
А вот Андрей Андреевич
Марков, советский математик, дал следующее определение для алгоритма. Алгоритм
– это точное предписание, определяющее вычислительный процесс, идущий от
варьируемых исходных данных к искомому результату.
Несмотря на то, что было
много вариаций определения алгоритма, все они сводились к одним и тем же требованиям:
·
алгоритм
должен содержать конечное количество простых для выполнения команд, то есть
удовлетворять требованию конечности записи;
·
алгоритм
должен выполнять конечное количество шагов при решении задачи, то есть
удовлетворять требованию конечности действий;
·
алгоритм
должен быть единым для всех допустимых исходных данных, то есть удовлетворять
требованию универсальности;
·
алгоритм
должен приводить к правильному по отношению к поставленной задачи решению, то
есть удовлетворять требование правильности.
В 1930-х гг. возникает
новая наука – теория алгоритмов. Она занимается изучением алгоритмов. Главным
толчком для этого была работа Курта Гёделя, австрийского логика, математика и
философа математики.
Он сформулировал и
доказал теоремы о неполноте. Его работы были опубликованы в 1931 году. В
теореме о неполноте символических логик было показано, что некоторые
математические проблемы не могут быть решены при помощи алгоритмов. Эта работа
дала толчок к поиску и анализу различных формализаций алгоритма.
Основной вопрос, на
который ищет ответ теория алгоритмов таков: для всякой ли задачи обработки
информации может быть построен алгоритм решения? Для того, чтобы найти ответ на
этот вопрос нужно было изначально договориться об исполнителе, на которого
будет ориентирован алгоритм.
Алан Тьюринг, английский
математик, логик, криптограф, предложил в качестве исполнителя машину Тьюринга.
Машина использовалась для
расшифровки сообщений. На основе открытого текста (стандартные отрывки текста,
значение которых известно аналитику), машина Тьюринга искала возможные
настройки, использованные для шифрования сообщений. Она производила ряд
логических предположений, основываясь на открытом тексте, а затем находила
противоречия, отбрасывала набор параметров и переходила к следующему. Таким
образом, большая часть всевозможных наборов отсеивалась и для более тщательного
анализа оставалось всего несколько вариантов. В 1940 году была запущена такая
первая машина.
В 1936–1937 годах
американский математик и логик, Эмиль Пост описал другую модель алгоритмической
машины. Она называется машиной Поста.
Можно сказать, что эта
машина является более упрощённой версией машины Тьюринга. Работа машины Поста основана
на двоичном алфавите. Поэтому она представляет для нас наибольший интерес, так
как все компьютеры работают с двоичным алфавитом. Более подробно с этой машиной
мы познакомимся чуть позже.
Язык программирования
алгоритмических машин представляет собой описание конечного
числа простых команд, которые могут быть реализованы в автоматическом устройстве.
Таким образом, система
команд исполнителя (СКИ) – это совокупность всех команд языка исполнителя.
Алгоритм управления
работой алгоритмической машины – это конечная
последовательность команд, с помощью которой машина решает задачу обработки
информации.
Для алгоритма управления
такой машиной существуют свои требования:
·
Дискретность. Этот пункт говорит о
том, что исполнитель должен выполнять каждый шаг отдельно от других;
·
Понятность. В алгоритме
используются только команды СКИ, предназначенные конкретно для этого
исполнителя;
·
Точность. Каждая команда должна
конкретно говорить о действии, которое должен выполнять исполнитель;
·
Конечность. Для исполнителя должно
быть задано определённое (конечное) число шагов, после выполнения которых
должен получится искомый результат.
Рассмотрим пример. Нам
необходимо записать алгоритм перемещения исполнителя Робот в клетку с домом.
Данному исполнителю доступны три команды: вперёд, налево и направо.
Итак, наш алгоритм будет
звучать следующим образом:
·
вперёд;
·
вперёд;
·
вперёд;
·
налево;
·
вперёд;
·
направо;
·
вперёд;
·
вперёд;
·
направо;
·
вперёд;
·
вперёд;
·
налево;
·
вперёд;
·
вперёд;
·
вперёд.
При выполнении этого
алгоритма исполнитель Робот дошёл до клетки с домом. В этом алгоритме мы с вами
можем увидеть все вышеприведённые требования. Давайте разберёмся.
Дискретность.
Исполнитель будет выполнять каждый шаг отдельно от других, так как, например,
он не сможет одновременно идти вперёд и выполнять поворот.
Далее идёт критерий «Понятность».
То есть в алгоритме должны использоваться только команды, которые поймёт данный
исполнитель. Так, например, в нашем случае нельзя было бы использовать команду
«Назад», иначе исполнитель бы просто не понял, что мы хотим этим сказать,
потому что такой команды в его системе нет по условию.
Следующий пункт «Точность».
В нашем алгоритме все действия записаны в том порядке, в котором нужно их
выполнять, и записаны конкретные команды для выполнения действий.
И последний критерий «Конечность».
У нас задано определённое количество ходов, после выполнения которых
исполнитель робот попадёт в клетку, где находится дом.
Таким образом мы можем
видеть, что в составленном алгоритме действий соблюдены все требования для
управления исполнителем.
Также необходимо различать
такие понятия, как команда и шаг.
Команда
– это отдельная инструкция в описании алгоритма.
А шаг алгоритма –
это отдельное действие, которое исполнитель выполняет по команде.
Давайте разберёмся на
примере. Мама попросила Катю помочь собрать ягоды малины.
Девочка взяла корзину и
подошла к кусту.
Она срывала ягоду и
опускала её в корзину. Так Катя делала до тех пор, пока на кусте не осталось ни
одной ягоды.
Из этих ягод сварили
варенье.
Записать действия Кати в
виде блок-схемы.
Рисуем овал и впишем в
него слово начало. Затем будет идти блок процесса. Впишем внутрь первое
действие «Взять корзину». Далее снова идёт блок процесса. Впишем в него
словосочетание «Подойти к кусту». Затем Катя должна посмотреть есть ли на кусте
ягода. Для этого нарисуем блок принятия решения и впишем в него вопрос «Куст с
ягодами?». От блока будут идти две стрелки «Да» и «Нет». Если идти по стрелке «Да»,
то у нас снова будут два блока процесса, в которых будут записаны следующие действия:
«Сорвать ягоду», «Положить в корзину», после чего возвращаемся к нашему блоку
принятия решения. Катя будет выполнять все эти действия до тех пор, пока куст
не опустеет. Тогда в блоке принятия решения с вопросом «Куст с ягодами?» мы
получим ответ «Нет». Идём по стрелке, после которой будет идти блок процесса, где
будет написано «Сварить варенье». Конец.
У нас получилась
блок-схема с циклическим алгоритмом. Мы можем видеть, что если выполнить данную
блок-схему для этого рисунка, то число команд у нас будет меньше, чем число
шагов, так как действия «Сорвать ягоду» и «Положить в корзину» будут
повторяться несколько раз.
Пришла пора подвести
итоги урока. Сегодня мы с вами узнали, что в 1930-х годах были предложены две
модели алгоритмических машин в теории алгоритмов: машина Тьюринга и машина
Поста. Для нас наибольший интерес представляет машина Поста, так как работа
этой машины основана на двоичном алфавите.
Также сегодня мы с вами
узнали, что любой алгоритм должен обладать следующими свойствами: дискретность
(каждый шаг алгоритма выполняется отдельно от других), понятность (в алгоритме
используются только команды из СКИ), точность (каждая команда определяет
однозначное действие исполнителя), конечность (за конечное число шагов
алгоритма получается искомый результат).
Not your computer? Use Guest mode to sign in privately. Learn more about using Guest mode
Основы алгоритмизации и технологии программирования
Понятие алгоритма и его свойства
Каждый из нас постоянно решает множество задач: как быстрее обраться на работу, как лучше спланировать дела текущего дня и многие другие. Некоторые задачи мы решаем автоматически, так как на протяжении многих лет привыкли к их выполнению, другие требуют длительного размышления над решением, но в любом случае, решение каждой задачи всегда делится на простые действия.
Алгоритм – описанная на некотором языке точная конечная система правил, определяющая содержание и порядок действий над некоторыми объектами, строгое выполнение которых дает решение, поставленной задачи. Понятие алгоритма, являющееся фундаментальным в математике и информатике, возникло задолго до появления средств вычислительной техники. Слово «алгоритм» появилось в средние века, когда европейцы познакомились со способами выполнения арифметических действий в десятичной системе счисления, описанными узбекским математиком Муххамедом бен Аль-Хорезми («аль-Хорезми» — человек из города Хорезми); в настоящее время город Хива в Хорезмской области Узбекистана). Слово алгоритм – есть результат европейского произношения слов аль-Хорезми. Первоначально под алгоритмом понимали способ выполнения арифметических действий над десятичными числами. В дальнейшем это понятие стали использовать для обозначения любой последовательности действий, приводящей к решению поставленной задачи.
Любой алгоритм существует не сам по себе, а предназначен для определенного исполнителя (человека, робота, компьютера, языка программирования и т.д.). Свойством, характеризующим любого исполнителя, является то, что он умеет выполнять некоторые команды. Совокупность команд, которые данный исполнитель умеет выполнять, называется системой команд исполнителя. Алгоритм описывается в командах исполнителя, который будет его реализовывать. Объекты, над которыми исполнитель может совершать действия, образуют так называемую среду исполнителя. Исходные данные и результаты любого алгоритма всегда принадлежат среде того исполнителя, для которого предназначен алгоритм.
Значение слова «алгоритм» очень схоже со значениями слов «рецепт», «метод», «процесс». Однако, в отличие от рецепта или процесса, алгоритм характеризуется следующими свойствами: дискретностью, массовостью, определенностью, результативностью, формальностью.
Дискретность (разрывность – противоположно непрерывности) – это свойство алгоритма, характеризующее его структуру: каждый алгоритм состоит из отдельных законченных действий, говорят: «Делится на шаги».
Массовость – применимость алгоритма ко всем задачам рассматриваемого типа, при любых исходных данных. Например, алгоритм решения квадратного уравнения в области действительных чисел должен содержать все возможные исходы решения, т.е., рассмотрев значения дискриминанта, алгоритм находит либо два различных корня уравнения, либо два равных, либо делает вывод о том, что действительных корней нет.
Определенность (детерминированность, точность) – свойство алгоритма, указывающее на то, что каждый шаг алгоритма должен быть строго определен и не допускать различных толкований; также строго должен быть определен порядок выполнения отдельных шагов. Помните сказку про Ивана-царевича? «Шел Иван-царевич по дороге, дошел до развилки. Видит большой камень, на нем надпись: «Прямо пойдешь – голову потеряешь, направо пойдешь – жену найдешь, налево пойдешь – разбогатеешь. Стоит Иван и думает, что дальше делать». Таких инструкций алгоритм содержать не может.
Результативность – свойство, состоящее в том, что любой алгоритм должен завершаться за конечное (может быть очень большое) число шагов. Вопрос о рассмотрении бесконечных алгоритмов остается за рамками теории алгоритмов.
Формальность – это свойство указывает на то, что любой исполнитель, способный воспринимать и выполнять инструкции алгоритма, действует формально, т.е. отвлекается от содержания поставленной задачи и лишь строго выполняет инструкции. Рассуждать «что, как и почему» должен разработчик алгоритма, а исполнитель формально (не думая) поочередно исполняет предложенные команды и получает необходимый результат.
Способы описания алгоритмов
Рассмотрим следующие способы описания алгоритма: словесное описание, псевдокод, блок-схема, программа.
Словесное описание представляет структуру алгоритма на естественном языке. Например, любой прибор бытовой техники (утюг, электропила, дрель и т.п.) имеет инструкцию по эксплуатации, т.е. словесное описание алгоритма, в соответствии которому данный прибор должен использоваться.
Никаких правил составления словесного описания не существует. Запись алгоритма осуществляется в произвольной форме на естественном, например, русском языке. Этот способ описания не имеет широкого распространения, так как строго не формализуем (под «формальным» понимается то, что описание абсолютно полное и учитывает все возможные ситуации, которые могут возникнуть в ходе решения); допускает неоднозначность толкования при описании некоторых действий; страдает многословностью.
Псевдокод – описание структуры алгоритма на естественном, частично формализованном языке, позволяющее выявить основные этапы решения задачи, перед точной его записью на языке программирования. В псевдокоде используются некоторые формальные конструкции и общепринятая математическая символика.
Строгих синтаксических правил для записи псевдокода не существует. Это облегчает запись алгоритма при проектировании и позволяет описать алгоритм, используя любой набор команд. Однако в псевдокоде обычно используются некоторые конструкции, присущие формальным языкам, что облегчает переход от псевдокода к записи алгоритма на языке программирования. Единого или формального определения псевдокода не существует, поэтому возможны различные псевдокоды, отличающиеся набором используемых слов и конструкций.
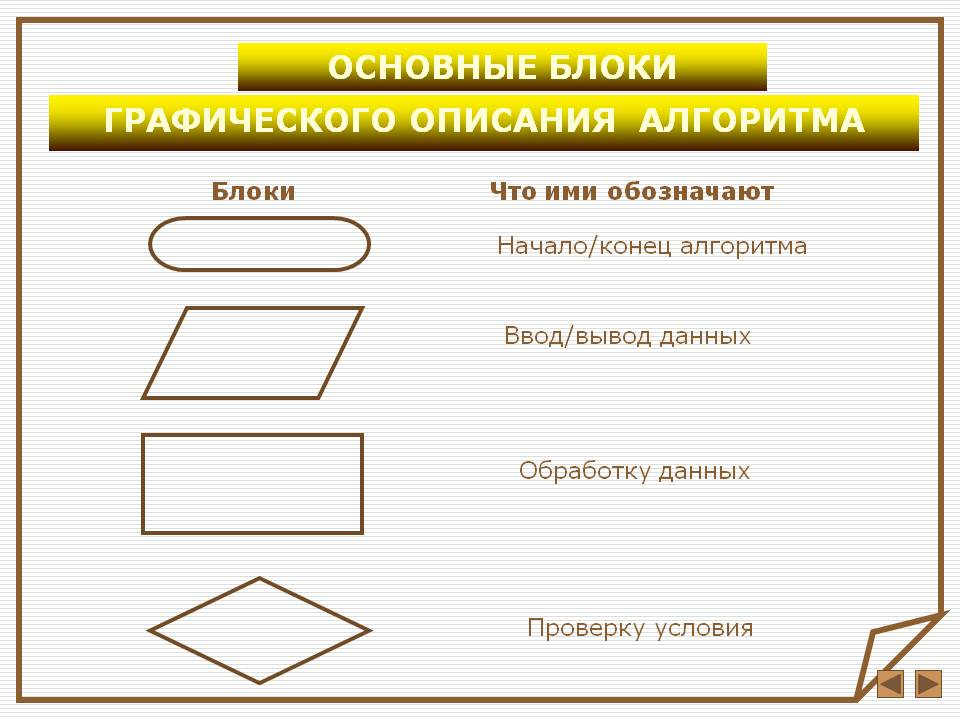
Блок-схема – описание структуры алгоритма с помощью геометрических фигур с линиями-связями, показывающими порядок выполнения отдельных инструкций. Этот способ имеет ряд преимуществ. Благодаря наглядности, он обеспечивает «читаемость» алгоритма и явно отображает порядок: выполнения отдельных команд. В блок-схеме каждой формальной конструкции соответствует определенная геометрическая фигура или связанная линиями совокупность фигур.
Рассмотрим некоторые основные конструкции, использующиеся для построения блок-схем (рис. 1).
(1) Блок, характеризующий начало/конец алгоритма (для подпрограмм – вызов/возврат);
(2) Блок — процесс, предназначенный для описания отдельных действий;
(3) Блок — предопределенный процесс, предназначенный для обращения к вспомогательным алгоритмам (подпрограммам);
(4) Блок — ввода/вывода с неопределенного носителя;
(5) Блок — ввод с клавиатуры;
(6) Блок — вывод на монитор;
(7) Блок — вывод на печатающее устройство;
(8) Блок – решение (проверка условия или условный блок);
(9) Блок, описывающий блок с параметром;
(10) Блок – границы цикла, описывающий циклические процессы типа: «цикл с предусловием», «цикл с постусловием»;
Описания алгоритма в словесной форме, на псевдокоде или в виде блок-схемы допускают некоторый произвол при изображении команд. Вместе с тем она настолько достаточна, что позволяет человеку понять суть дела и исполнить алгоритм. На практике исполнителями алгоритмов выступают компьютеры. Поэтому алгоритм, предназначенный для исполнения на компьютере, должен быть записан на «понятном» ему языке, такой формализованный язык называют языком программирования.
Программа – описание структуры алгоритма на языке алгоритмического программирования. Программа на языке декларативного программирования представляет собой совокупность описанных знаний и не содержит явного алгоритма исполнения.
Основные алгоритмические конструкции
Элементарные шаги алгоритма можно объединить в следующие алгоритмические конструкции: линейные (последовательные), разветвляющиеся, циклические и рекурсивные.
Линейная алгоритмическая конструкция
Линейной называют алгоритмическую конструкцию, реализованную в виде последовательности действий (шагов), в которой каждое действие (шаг) алгоритма выполняется ровно один раз, причем после каждого i- гo действия (шага) выполняется (i+ 1)-е действие (шаг), если i-e действие – не конец алгоритма.
Пример 1.
Опишем алгоритм сложения двух чисел на псевдокоде в виде блок-схемы (рис. 2).
Псевдокод:
Ввод двух чисел а, b .
Вычисляем сумму S = а + b .
Вывод S.
Конец.
Разветвляющаяся алгоритмическая конструкция
Разветвляющейся (или ветвящейся) называется алгоритмическая конструкция, обеспечивающая выбор между двумя альтернативами в зависимости от значения входных данных. При каждом конкретном наборе входных данных разветвляющийся алгоритм сводится к линейному. Различают неполное (если – то) и полное (если – то – иначе) ветвления. Полное ветвление позволяет организовать две ветви в алгоритме (то или иначе), каждая из которых ведет к общей точке их слияния, так что выполнение алгоритма продолжается независимо от того, какой путь был выбран (рис. 3). Неполное ветвление предполагает наличие некоторых действий алгоритма только на одной ветви (то), вторая ветвь отсутствует, т.е. для одного из результатов проверки никаких действий выполнять не надо, управление сразу переходит к точке слияния (рис. 4).
Рассмотрим стандартный алгоритм поиска наибольшего (наименьшего) значения среди нескольких заданных. Основная идея алгоритма сводится к следующему: за наибольшее (наименьшее) принимаем значение любого из данных. Поочередно сравниваем оставшиеся данные с наибольшим (наименьшим). если окажется, что очередное значение входного данного больше (меньше) наибольшего (наименьшего), то наибольшему (наименьшему) присваиваем это значение. Таким образом, сравнив все входные данные, найдем наибольшее (наименьшее) среди них. Алгоритм использует неполное ветвление.
Пример 2.
Заданы три числа. Найти значение наименьшего из них Заданные числа обозначим: а, b, с; результирующее наименьшее – min. На рис. 5 представлена блок-схема алгоритма решения данной задачи.
Алгоритмическая конструкция «Цикл»
Циклической (или циклом) называют алгоритмическую конструкцию, в кoтoрoй некая, идущая подряд группа действий (шагов) алгоритма может выполняться несколько раз, в зависимости от входных данных или условия задачи. Группа повторяющихся действий на каждом шагу цикла называется телом цикла. Любая циклическая конструкция содержит себе элементы ветвящейся алгоритмической конструкции.
Рассмотрим три типа циклических алгоритмов: ц uкл с параметром (который называют арифметическим циклом), цикл с предусловием и цикл с постусловием (их называют итерационными) .
Арифметический цикл
В арифметическом цикле число его шагов (повторений) однозначно определяется правилом изменения параметра, которое задается с помощью начального (N) и конечного (К) значений параметра и шагом (h) его изменения. Т.е., на первом шаге цикла значение параметра равно N, на втором – N + h, на третьем – N + 2h и т.д. На последнем шаге цикла значение параметра не больше К, но такое, что дальнейшее его изменение приведет к значению, большему, чем К.
Пример 3.
Вывести 10 раз слово «Привет!».
Параметр цикла обозначим i, он будет отвечать за количество выведенных слов. При i=1 будет выведено первое слово, при i=2 будет выведено второе слова и т. д. Так как требуется вывести 10 слов, то последнее значение параметра i=10. В заданном примере требуется 10 раз повторить одно и то же действие: вывести слово «Привет!». Составим алгоритм, используя арифметический цикл, в котором правило изменения параметра i=1,10, 1. т. е. начальное значение параметра i=1; конечное значение i=10; шаг изменения h=1. На рис. 6 представлена блок-схема алгоритма решения данной задачи.
Цикл с предусловием
Количество шагов цикла заранее не определено и зависит от входных данных задачи. В данной циклической структуре сначала проверяется значение условного выражения (условие) перед выполнением очередного шага цикла. Если значение условного выражения истинно, исполняется тело цикла. После чего управление вновь передается проверке условия и т.д. Эти действия повторяются до тех пор, пока условное выражение не примет значение ложь. При первом же несоблюдении условия цикл завершается.
Блок-схема данной конструкции представлена на рис. 7 двумя способами: с помощью условного блока а и с помощью блока границы цикла б. Особенностью цикла с предусловием является то, что если изначально условное выражение ложно, то тело цикла не выполнится ни разу.
Цикл с постусловием
Как и в цикле с предусловием, в циклической конструкции с постусловием заранее не определено число повторений тела цикла, оно зависит от входных данных задачи. В отличие от цикла с предусловием, тело цикла с постусловием всегда будет выполнено хотя бы один раз, после чего проверяется условие. В этой конструкции тело цикла будет выполняться до тех пор, пока значение условного выражения ложно. Как только оно становится истинным, выполнение команды прекращается. Блок-схема данной конструкции представлена на рис. 8 двумя способами: с помощью условного блока а и с помощью блока управления б.
Рекурсивный алгоритм
Рекурсивным называется алгоритм, организованный таким образом, что в процессе выполнения команд на каком-либо шаге он прямо или косвенно обращается сам к себе.
Простые типы данных: переменные и константы
Реальные данные, которые обрабатывает программа, — это целые и вещественные числа, символы и логические величины. Эти простые типы данных называют базовыми. Все данные, обрабатываемые компьютером, хранятся в ячейках памяти компьютера, каждая из которых имеет свой адрес. Для того чтобы не следить за тем, по какому адресу будут записаны те или иные данные, в языках программирования используется понятие переменной, позволяющее отвлечься от адреса ячейки памяти и обращаться к ней с помощью имени (идентификатора).
Переменная – есть именованный объект (ячейка памяти), который может изменять свое значение. Имя переменной указывает на зн ачение, а способ ее хранения и адрес остаются скрытыми от программиста. Кроме имени и значения, переменная имеет тип, определяющий, какая информация находится в памяти. Тип переменной задает:
-
используемый способ записи информации в ячейки памяти;
-
необходимый объем памяти для ее хранения.
Объем памяти для каждого типа определяется таким образом, чтобы в него можно было поместить любое значение из допустимого диапазона значений данного типа. Например, тип «байт» может принимать значения от О до 255, что в двоичном коде (255(10)=11111111(2)) соответствует ячейке памяти длиной в 8 бит (или 1 байт).
В описанных выше алгоритмах (примеры 1-3) все данные хранятся в виде переменных. Например, инструкция «Ввод двух чисел а, b » означает введение пользователем значений двух переменных, а инструкция «К=К + 1» означает увеличение значения переменной К на единицу.
Если переменные присутствуют в программе, на протяжении всего времени ее работы – их называют статическими. Переменные, создающиеся и уничтожающиеся на разных этапах выполнения программы, называют динамическими.
Все остальные данные в программе, значения которых не изменяются на протяжении ее работы, называют константами или постоянными. Константы, как и переменные, имеют тип. Их можно указывать явно, например, в инструкции «К=К+1» 1 есть константа, или для удобства обозначать идентификаторами: pi=3,1415926536. Только значение pi нельзя изменить, так как это константа, а не переменная.
Структурированные данные и алгоритмы их обработки
Для повышения производительности и качества работы необходимо иметь данные, максимально приближенные к реальным аналогам. Тип данных, позволяющий хранить вместе под одним именем несколько переменных, называется структурированным. Каждый язык программирования имеет свои структурированные типы. Рассмотрим структуру, объединяющую элементы одного типа данных, — массив.
Массивом называется упорядоченная совокупность однотипных величин, имеющих общее имя, элементы которой адресуются (различаются) порядковыми номерами (индексами). В качестве иллюстрации можно представить шкаф, содержащий множество пронумерованных ящиков (совокупность — «Ящик № 1», «Ящик № 2», «Ящик № 3» и т.д.; «Ящик» — общее имя всех ее элементов). Доступ к содержимому конкретного ящика (элементу массива) осуществляется после выбора ящика по его номеру (индексу). Элементы массива в памяти компьютера хранятся по соседству, одиночные элементы простого типа такого расположения данных в памяти не предполагают. Массивы различаются количеством индексов, определяющих их элементы.
Одномерный массив (шкаф ящиков в один ряд) предполагает наличие у каждого элемента только одного индекса. Примерами одномерных массивов служат арифметическая (аi) и геометрическая (bi) последовательности, определяющие конечные ряды чисел. Количество элементов массива называют размерностью. При определении одномерного массива его размерность записывается в круглых скобках, рядом с его именем. Например, если сказано: «задан массив A (10)», это означает, что даны элементы: a 1 , a 2 , …, a 10 . Рассмотрим алгоритмы обработки элементов одномерных массивов.
Ввод элементов одномерного массива осуществляется поэлементно, в порядке, необходимом для решения конкретной задачи. Обычно, когда требуется ввести весь массив, порядок ввода элементов не важен, и элементы вводятся в порядке возрастания их индексов. Алгоритм ввода элементов массива А(10) представлен на рис.9.
Пример 4.
В заданном числовом массиве A(l0) найти наибольший элемент и его индекс, при условии, что такой элемент в массиве существует, и единственный.
Обозначим индекс наибольшего элемента т. Будем считать, что первый элемент массива является наибольшим (т = 1). Сравним поочередно наибольший с остальными элементами массива. Если оказывается, что текущий элемент массива а i (тот, c которым идет сравнение) больше выбранного нами наибольшего ат, то считаем его наибольшим (т=i) (рис.10).
Рассмотрим двумерный массив (шкаф с множеством ящиков, положение которых определяется двумя координатами – по горизонтали и по вертикали). В математике двумерный массив (таблица чисел) называется матрицей. Каждый ее элемент имеет два индекса а ij , первый индекс i определяет номер строки, в которой находится элемент (координата по горизонтали), а второй j – номер столбца (координата по вертикали). Двумерный массив характеризуется двумя размерностями N и М, определяющими число строк и столбцов соответственно (рис. 11).
Ввод элементов двумерного массива осуществляется построчно, в свою очередь, ввод каждой строки производится поэлементно, тем самым определяется циклическая конструкция, реализующая вложение циклов. Внешний цикл определяет номер вводимой строки ( i ), внутренний – номер элемента по столбцу ( j ). На рис. 12 представлен алгоритм ввода матрицы A(MxN) .
Пример 5.
Задана матрица символов (100х100), представляющая собой карту ночного неба; звездам на карте соответствует символы «*». Определить: сколько звезд на карте?
Алгоритм решения задачи достаточно прост, необходимо перебрать все элементы матрицы и посчитать, сколько среди них символов «*». Обозначим К переменную – счетчик. На рис 13. представлена блок-схема решения этой задачи.
1. ТО-201 16.11.2020
Алгоритм, его свойства, способы
описания.
Программный принцип работы
компьютера
2.
Что такое алгоритм?
Алгоритм — это сформулированное на некотором языке
правило, указывающее на действия, последовательное
выполнение которых приводит от исходных данных к
искомому результату. Значение слова алгоритм очень схоже
со значением слов рецепт, процесс, метод, способ. Однако
любой алгоритм, в отличие от рецепта или способа,
обязательно обладает следующими свойствами.
Алгоритм — это предписание исполнителю (человеку или
автомату)
выполнить
точно
определенную
последовательность действий, направленных на достижение
заданной цели.
3.
4. Свойства алгоритма:
Понятность — алгоритм должен быть записан на понятном для
исполнителя языке;
Конечность (результативность) — выполняемый алгоритм
должен приводиться к результату за конечное число шагов;
Дискретность- любой алгоритм должен состоять из конкретных
действий, следующих в определенном порядке;
Массовость- один и тот же алгоритм можно использовать с
различными исходными данными;
Детерминированность (определенность) – каждая команда
алгоритма (предписание, выдаваемое на каждом шагу) должна
быть понятна исполнителю, не оставлять места для ее
неоднозначного толкования и неопределенного исполнения.
5. Способы записи алгоритма
1. С помощью рисунка (например, процесс подключения монитора);
2. На естественном языке – построчно, каждая команда – с новой
строки (последовательность проявления фотопленки,
последовательность склеивания поверхностей на тюбике с клеем и
т.д.);
3. Использование псевдокода – некоторую систему обозначений и
правил.
Псевдокод
занимает
промежуточное
место
между
естественным и формальным языками. Единого или формального
определения псевдокода не существует, поэтому возможны различные
псевдокоды, отличающиеся набором служебных слов и основных
(базовых) конструкций (например, школьный АЯ).
4. Графическое представление – блок-схема.
6. Блок- схема
Блок-схема – это совокупность
геометрических фигур, каждая из которых
описывает какое-либо действие в алгоритме.
7.
8. Основные типы алгоритмических структур:
Линейная
Разветвляющаяся
Циклическая
9. Линейный алгоритм
Линейные алгоритмы, в которых все действия совершаются одно за
другим, независимо от исходных данных и результатов
промежуточных вычислений. Характерная форма для линейного
алгоритма – последовательное выполнение команд.
10. Разветвляющийся алгоритм
Разветвляющимся называют алгоритм, в котором в зависимости от
исходных данных и результатов промежуточных вычислений
осуществляется выбор по одному из возможных вариантов.
Варианты
(направления
вычислений),
по
которым
может
реализоваться вычислительный процесс, называют ветвями. Выбор
ветви зависит от результатов проверки некоторого условия. Если
условие выполняется, то выбирается одна ветвь, если не
выполняется, то другая ветвь.
11.
Разветвляющийся алгоритм может быть в полной или
неполной форме
Неполная форма
Полная форма
12.
Из нескольких ветвлений можно сконструировать структуру «выбор»
(множественное ветвление), которая будет выбирать не из двух, а из
большего количества вариантов действий исполнителя, зависящих от
нескольких условий. Существенно, что выполняется только одна ветвь
— в такой структуре важное значение приобретает порядок следования
условий: если выполняются несколько условий, то сработает только
одно из них — первое сверху.
13. Циклические алгоритмы
Циклическим называют алгоритм, в котором получение результата
обеспечивается многократным выполнением одних и тех же операций.
Цикл – многократно повторяющийся участок вычислительного процесса.
В
цикле
всегда
имеется
четыре
действия:
подготовка – задание начального значения параметру цикла;
основные действия (тело цикла) – реализация необходимых вычислений;
подготовка к следующему циклу (модификация) – изменение параметра
цикла;
проверка
условия
–
проверка
условия
окончания
цикла.
Способ организации цикла зависит от условия задачи. Иногда
указывается количество повторений цикла. Это так называемые циклы
со
счетчиками
(или
арифметические
алгоритмы)
.
14. Типы циклических алгоритмов:
Цикл с предусловием. Перед выполнением цикла проверяется условие
выполнения цикла. Если условие истинно, то цикл выполняется. При
ложности условия цикл заканчивается.
Цикл с постусловием. Условие продолжения цикла проверяется уже после
того, как выполнено тело цикла.
Основное различие: во втором случае цикл выполняется, по крайней мере,
один раз, а в первом – может получиться, что цикл вообще не выполняется.
Цикл с заданным числом повторений, когда указывается количество
повторений цикла. Это так называемые циклы со счетчиками (или
арифметические циклы).
Итерационный цикл используется, когда задана точность вычисления
результата. В таком цикла на каждом шаге (итерации) происходит
постепенное уточнение результата. В большинстве задач вычислительный
процесс, реализующий алгоритм, является комбинированным, т.е. он
содержит разветвления, является циклическим, или итерационным.
.
15.
Отметим разницу между понятиями «команда алгоритма» и
«шаг алгоритма». Команда — это отдельная инструкция в
описании алгоритма, а шаг алгоритма — это отдельное действие,
которое исполнитель выполнит по команде. В циклических
алгоритмах число шагов при выполнении алгоритма может быть
больше, чем число команд в алгоритме, за счет повторного
выполнения одних и тех же команд.
x1
… xn
условие 1
… условие n
формула 1
…
формула n
16.
Вычислить площадь и периметр прямоугольника
начало
Ввести a, b
S = a*b
Р = (a+b)*2
Вывести S, Р
конец
17. Вычисления значения гипотенузы прямоугольного треугольника, если известны значения его катетов
начало
Ввести a, b
с = √ a2+b2
Вывести с
конец
18. Вычислить функцию, заданную в зависимости от значения аргумента
начало
Х <1
Y = 2x+1
Y = 3x — 1
конец
19. Составить блок-схему определения значения функции у = √ х, при х – неотрицательном.
начало
Х >=0
у=√х
не сущ-ет
конец
20. Сумма чисел из промежутка от 5 до 10
начало
S=0
начало
А= 5 : S = 0
а от 5 до 10
a < 11
s=s+a
s=s+a
конец
конец
21. Произведение всех чисел из промежутка от 5 до 10
начало
S=1
а от 5 до 10
s=s*a
конец
начало
А= 5 : S = 1
a < 11
s=s*a
конец
22. Попробуйте сформулировать известную русскую пословицу по ее блок-схеме
Препятствие в виде
возвышенности
да
обход
умный?
нет
восхождение
23. Попробуйте сформулировать известную русскую пословицу по ее блок-схеме
да
нет
Лето?
да
Сани
Телега
Зима?
нет
24. Попробуйте сформулировать известную русскую пословицу по ее блок-схеме
I=0
I=I+1
I 7
нет
да
Отмерь
Отрежь
25. Определить результат работы алгоритма, представленного в виде блок-схемы
начало
ввод числа
да
нет
> 10
-4
да
+1
< 15
+3
нет
да
-2
-6
вывод числа
конец
>8
нет
-7
26. Составьте блок-схему по высказыванию
«Если мысль нельзя выразить
простыми словами, значит, она
ничтожна и надо ее отбросить.»
27. Составить блок-схему к задаче: В корзине имеются белые и черные шары. Нужно белые шары положить в белую коробку, а черные – в
черную.
28. Определить значение переменной a после выполнения фрагмента алгоритма
а:= 16
b:= 2
да
b:= 32
нет
b:= b*2
a:= a+2
29. Определить значение переменных х и у после выполнения фрагмента алгоритма
x:= 5
y:= 10
нет
x <10
да
да
x<y
нет
x:= x-5
y:= y+5
x:= x+1
y:= y-1
30. Определить значение переменной х после выполнения фрагмента алгоритма
х:= 136
у:= 72
да
х=у
нет
да
x>y
x:= x-y
нет
y:= y-x
31.
Определить значение переменной n после
выполнения фрагмента алгоритма
n:= 10
m:= 12
да
m<6
нет
m:= m – 2
n:= n*2
32.
Определить значения целочисленных переменных х и у
после выполнения фрагмента алгоритма
x:= 15
y:= 35
нет
x < 30
да
да
x>y
нет
x:= x+10
y:= y-10
x:= x-5
y:= y+5
33. Программный принцип работы компьютера
Компьютер – двуединая система, состоящая из
аппаратной части (технических устройств) и
информационной
части
(программного
обеспечения):
КОМПЬЮТЕР
АППАРАТУРА
= (hardware)
ПРОГРАММНОЕ
+ ОБЕСПЕЧЕНИЕ
(software)
34. Программное обеспечение (ПО)
ПО – это совокупность программ, хранящихся на
устройствах долговременной памяти компьютера и
предназначенных для массового использования.
Использование компьютера человеком происходит
по схеме:
ЗАДАЧА
ВЫБОР И
ИНИЦИАЛИЗАЦИЯ
ПРОГРАММЫ
РАБОТА
35. Программы и данные
Программное обеспечение – это не только собственно
программы, но и данные, с которыми работают эти
программы.
Данные и программы хранятся на дисках, в отдельных
файлах.
Часто объем данных во много раз превышает размер
программ.
36.
Программное обеспечение (ПО)
Системное ПО
Операционные системы:
— Однозадачные (MS DOS )
— Многозадачные (Unix,
Windows и др. )
Сервисные программы
Прикладное ПО
Текстовые редакторы
(MS Word, WordPad и др. )
Графические редакторы
(Adobe Rhotoshop, Corel
Draw, MS Paint и др. )
Электронные таблицы
(MS Excel и др. )
Среды разработки
Интегрированные
(Visual Studio, Eclipse,
XCode, RAD )
Поддерживающие только
конкретный язык
программирования
(Borland C++, DrJava,
Delphi )
37. Этапы решения задачи на компьютере
Работа по решению любой задачи с использованием компьютера
делится на следующие этапы:
1.Постановка задачи.
2.Формализация задачи (формальное математическое описание
алгоритма).
3.Построение алгоритма.
4.Составление программы на языке программирования.
5.Отладка и тестирование программы.
6.Проведение расчетов и анализ полученных результатов.
Часто эту последовательность называют технологической
цепочкой решения задачи на компьютере.
38.
Вся наша жизнь – это алгоритм
сложной структуры.
Надо стремиться к тому, чтобы
каждое наше действие было
обдуманным и приводило к
правильному, достойному
результату!
Источник статьи
Автор24
— учеба по твоим правилам
Решение задач с использованием компьютера основано на понятии алгоритма, который является точным описанием вычислительного процесса, ведущего от варьируемых начальных данных к конечному результату.
Алгоритмы заложены в основе каждой программы, а также они встречаются во многих сферах деятельности человека (например, рецепты, схема вязания или танца).
Понятие алгоритма
Определение 2
Алгоритм представляет собой точное описание определенного процесса, инструкцию по его выполнению.
Процесс разработки алгоритма — достаточно сложный и трудоемкий.
Можно также сказать, что алгоритм представляет собой конечную последовательность команд для исполнителя, направленную на достижение конкретной цели.
Цель же, в свою очередь, является достижением желаемого результата.
В качестве исполнителя могут выступать люди, живые существа, автоматические устройства, способные к исполнению и восприятию команд.
Определение 3
Перечень команд, воспринимаемых и выполняемых (по возможности) исполнителем, называют системой команд.
Каждый алгоритм предназначен для конкретного исполнителя. Исполнение алгоритма начинается с первой команды. После того, как ее исполнили, переходят к следующей команде и так до конца алгоритма.
В качестве примера алгоритма можно вспомнить известный всем со школы арифметический способ сложения двух положительных чисел «столбиком». Алгоритм данной задачи представим в виде системы следующих действий:
- выделим в слагаемых разряды единиц и сложим единицы;
- при получении суммы меньшей 10 запишем ее в разряде единиц под нижним числом;
- при получении суммы большей или равной 10 запишем в разряде единиц только количество единиц, затем выделим в слагаемых разряд десятков и запишем полученный при сложении единиц десяток над разрядом десятков первого (верхнего) слагаемого;
- сложим десятки и т. д.
«Алгоритмизация. Понятие алгоритма. Свойства и способы описания алгоритмов.» 👇
Аналогичные указания дают для сложения единиц других разрядов числа. Системой-исполнителем этого алгоритма может стать как ЭВМ, так и человек.
Понятие алгоритма в теорию и практику обучения вошло в конце $50$-х годов прошлого столетия в связи с развитием программированного обучения и применением обучающимися машин.
Способы описания алгоритмов
Существуют различные способы описания алгоритмов. Приведем основные из них:
- словесный (пошаговое описание);
- табличный и в виде формул;
- графический (в виде схем);
- с использованием псевдокода (алгоритмического языка).
Алгоритмический язык является формальным языком, предназначенным для записи алгоритма. В его состав входят набор основных символов (алфавит), система точных правил построения текстов (синтаксис) и система соответствия синтаксически допустимых текстов языка описываемым действиям и объектам (семантика).
Множество языков программирования, используемых при ре¬шении задач на ЭВМ, являются алгоритмическими.
Псевдокод представляет собой способ описания логики программы до начала ее программирования и занимает промежуточное положение между машинным языками и естественными.
Под схемой алгоритма понимают графическое пред¬ставление последовательности шагов алгоритма, наглядно показывающее взаимосвязь опера¬ций, которые осуществляются в алгоритме на каждом шаге, и их очередность. Другими словами, для графического изображения структуры алгоритма используется блок-схема.
В соответствии с блок-схемой последовательность действий указывается с по¬мощью стрелок, которые соединяют отдельные блоки и показывают, какой блок и за каким должен быть выполнен.
Свойства алгоритмов
Существует ряд определенных требований к алгоритмам. Перечислим семь важных свойств, которыми должен обладать каждый алгоритм:
- Наличие ввода исходных данных.
- Наличие вывода результата выполнения.
- Однозначность, так как компьютеру понятны лишь однозначные инструкции.
- Общность, в соответствии с которой алгоритм может использоваться не только для решения одной задачи, но и целого класса задач.
- Корректность, согласно которой при выполнении алгоритма должно быть всегда правильное решение задачи.
- Конечность означает, что решение задачи необходимо получить за конечное число шагов.
- Эффективность означает, что для решения задачи необходимо использовать ограниченные ресурсы компьютера (объем оперативной памяти, процессорное время и т. д.).
Эффективность алгоритма определяют с учетом потребляемых ресурсов компьютера, к которым относят быстродействие (количество выполняемых операций и затраты трудоемкости на каждую из них) и общий объем оперативной памяти, которая выделяется под данные. Приведенные показатели могут иногда быть противоречивыми: так в результате повышения быстродействия могут потребоваться дополнительные расходы памяти и наоборот. При возможности улучшения одного показателя без ущерба для другого необходимо этого добиваться. В случаях, когда возникает дилемма, рекомендуется предпочесть экономию памяти в ущерб производительности, поскольку тактовая частота процессоров растет опережающими темпами по сравнению с объемами оперативной памяти.
Специалистами предлагается ряд мер для повышения эффективности.
Блок-схемы
Основные алгоритмические структуры изображаются с помощью специальных графических символов. Все составляющие блок-схемы соединяются между собой в той последовательности, в какой они должны быть исполнены.
Кроме того, в алгоритмах используются разветвляющие и циклические блоки.
Обязательными блоками являются блоки начала и конца алгоритма. Между ними размещаются остальные блоки алгоритма.
Операторный блок (блок действия) содержит команды обработки данных.
Блок проверки условия предполагает 2 варианта дальнейшего развития решения задачи, в зависимости от того или иного выполнения поставленного условия.
Блоки ввода или вывода данных. Для выполнения алгоритма необходимы не только команды, но и данные, поступающие из вне. Для получения этих данных используется блок ввода. Для того, чтобы можно было вывести результат выполнения программы, либо какое-нибудь сообщение используют блок вывода.
Ниже на рисунке представлены графические изображения основных блоков алгоритма.